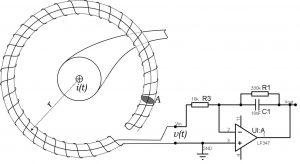
罗氏线圈（Rogowski线圈）是一种用于测量交流电流，尤其适用于高电流和脉冲电流的电磁传感器。其原理基于法拉第电磁感应定律，通过检测导体中电流变化所产生的磁场，从而间接测量电流大小和波形。

基本结构

罗氏线圈通常由一根紧密缠绕的导线绕制成的空心螺旋线圈组成，形状类似于一个开口的环状。线圈的截面积可以根据测量需求进行设计，但一般不闭合，这与传统的电流互感器不同。

工作原理

1. 电流产生磁场：当被测导体中有电流通过时，会在其周围产生变化的磁场。
2. 感应电压：根据法拉第电磁感应定律，变化的磁场会在罗氏线圈中感应出电压。具体来说，感应电压 $V(t)$ 与导体中电流 $I(t)$ 的变化率成正比：V(t)=N⋅μ0⋅A⋅dI(t)dtV(t)=N⋅μ0​⋅A⋅dtdI(t)​其中：
   • $N$ 是线圈的匝数
   • μ0μ0​ 是真空磁导率
   • $A$ 是线圈的有效面积
   • dI(t)dtdtdI(t)​ 是电流的变化率
3. 积分得到电流：由于感应电压与电流的变化率相关，需要通过积分电路将感应电压转换为与电流成正比的信号，以得到实际的电流值。

优点

• 高线性度：由于没有铁芯，避免了铁芯饱和带来的非线性失真，线性度高。
• 宽频带：适用于从直流到高频的广泛频率范围。
• 轻便且易于安装：罗氏线圈通常是柔性的，可以轻松绕在导体周围，无需截断被测导体。
• 低成本：相比传统的电流互感器，罗氏线圈结构简单，制造成本较低。

应用领域

• 电力系统：用于测量大电流、短路电流以及进行电力监测和保护。
• 脉冲电流测量：在电子设备和工业控制中，测量快速变化的脉冲电流。
• 科学研究：用于物理实验中需要高精度电流测量的场合。

注意事项

• 积分电路：需要配套高精度的积分电路，确保测量信号的准确性。
• 校准：为了确保测量精度，罗氏线圈需要定期校准，特别是在不同环境条件下使用时。

总结

罗氏线圈因其高线性度、宽频带和安装便利性，成为许多高电流和脉冲电流测量应用中的理想选择。正确理解其工作原理和特性，有助于在实际应用中充分发挥其优势，实现精准的电流测量。